|
|
|
Let ![]() be a Nonnegative Sequence and
be a Nonnegative Sequence and ![]() a Nonnegative integrable function. Define
a Nonnegative integrable function. Define
| (1) | |||
| (2) |
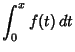 |
(3) | ||
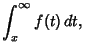 |
(4) |
| (5) |
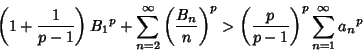 |
(6) |
References
Beesack, P. R. ``On Some Integral Inequalities of E. T. Copson.'' In General Inequalities 2
(Ed. E. F. Beckenbach). Basel: Birkhäuser, 1980.
Copson, E. T. ``Some Integral Inequalities.'' Proc. Royal Soc. Edinburgh 75A, 157-164, 1975-1976.
Hardy, G. H.; Littlewood, J. E.; and Pólya, G. Theorems 326-327, 337-338, and 345 in Inequalities.
Cambridge, England: Cambridge University Press, 1934.
Mitrinovic, D. S.; Pecaric, J. E.; and Fink, A. M.
Inequalities Involving Functions and Their Integrals and Derivatives. Dordrecht, Netherlands: Kluwer, 1991.